一条长为0.80m的轻绳一端固定在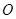
点，另一端连接一质量
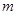=0.10kg的小球，悬点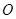距离水平地面的高度H = 1.00m。开始时小球处于
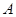点，此时轻绳拉直处于水平方向上，如图所示。让小球从静止释放，当小球运动到
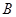点时，轻绳碰到悬点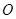正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失，取重力加速度g=10m/s2。求：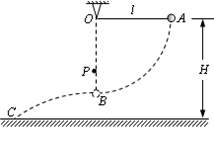 
（1）当小球运动到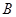点时的速度大小；
（2）绳断裂后球从点抛出并落在水平地面的C点，求C点与点之间的水平距离；
（3）若OP=0.6m，轻绳碰到钉子P时绳中拉力达到所能承受的最大拉力断裂，求轻绳能承受的最大拉力。
如图所示，光滑水平面上静止一质量为M=0.98kg的物块。紧挨平台右侧有传送带，与水平面成30°角，传送带底端A点和顶端B点相距L=3m。一颗质量为m=0.02kg的子弹，以
的水平向右的速度击中物块并陷在其中。物块滑过水平面并冲上传送带，物块通过A点前后速度大小不变。已知物块与传送带之间的动摩擦因数
，重力加速度g=10m/s2。
（1）如果传送带静止不动，求物块在传送带上滑动的最远距离；
（2）如果传送带匀速运行，为使物块能滑到B端，求传送带运行的最小速度。
（3）若传送带以某一速度匀速运行时，物块恰能以最短时间从A端滑到B端，求此过程中传送带与物块间产生的热量。
如图所示，在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场，第三象限有沿y轴负方向的匀强电场，第四象限内无电场和磁场．质量为m、带电量为q粒子从M点以速度V0沿x轴负方向进入电场，粒子先后经x轴上的N、P点。不计粒子的重力，设OM=OP=L，ON=2L，求：
（1）匀强电场的场强E；
（2）匀强磁场的磁感强度B的大小和方向。
电量为q质量为m的负粒子，由静止从电场边界上O点进入如图所示的电场、磁场，电场强度为E，磁感强度为B，电场宽度为L，磁场足够大。（不计带电粒子重力）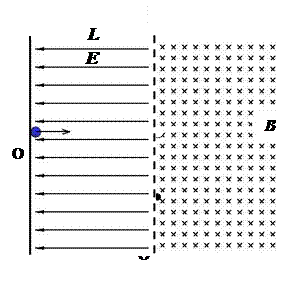
1）求带电粒子从O点出发后第一次到达电磁场边界时的速度；
2）求带电粒子从O点出发后到第二次到达电磁场边界时的时间；
3）求带电粒子从O点出发后到第三次到达电磁场边界过程中经过的路程；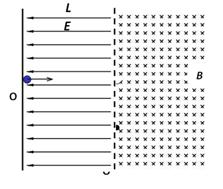
如图所示，水平放置的平行金属板的板长
，板间匀强电场的场强
，一束电子以初速度
沿两板中线垂直电场进入板间，从板最右端到竖立的荧光屏的距离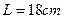
，求电子打在荧光屏上的光点偏离荧光屏中心O的距离Y。（电子的比荷
人造地球卫星常常利用太阳能电池作为电源，太阳能电池由许多片电池板组成。设某太阳能电池板的内电阻为r＝20Ω，它不接外电路时两极间的电压为8×10－4V。
（1）该太阳能电池板的电动势为多大？
（2）该太阳能电池板的短路电流为多大？
（3）若在该太阳能电池板的两极间连接一只定值电阻R，R＝5Ω，则电阻R两端的电压为多大？