已知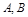 分别是椭圆
分别是椭圆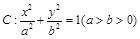 的左、右顶点,点
的左、右顶点,点 在椭圆
在椭圆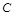 上,且直线
上,且直线 与直线
与直线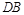 的斜率之积为
的斜率之积为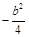 .
.
(Ⅰ)求椭圆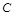 的方程;
的方程;
(Ⅱ)如图,已知 是椭圆
是椭圆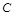 上不同于顶点的两点,直线
上不同于顶点的两点,直线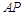 与
与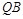 交于点
交于点 ,直线
,直线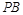 与
与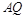 交于点
交于点 .① 求证:
.① 求证: ;② 若弦
;② 若弦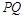 过椭圆的右焦点
过椭圆的右焦点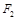 ,求直线
,求直线 的方程.
的方程.
(本题满分13分)
设椭圆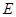 :
: 
 过
过 ,
, 两点,其中
两点,其中 为椭圆的
为椭圆的
离心率, 为坐标原点.
为坐标原点.
(I)求椭圆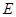 的方程;
的方程;
(II)过椭圆右焦点 的一条直线
的一条直线 与椭圆交于
与椭圆交于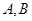 两点,若
两点,若 ,求弦
,求弦 的长.
的长.
(本题满分13分)
已知函数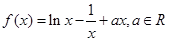 .
.
(I)若函数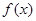 在
在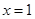 处的切线与
处的切线与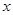 轴平行,求
轴平行,求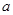 值;
值;
(II)讨论函数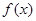 在其定义域内的单调性;
在其定义域内的单调性;
(III)定义:若函数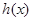 在区间D上任意
在区间D上任意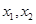 都有
都有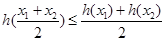 ,则称函数
,则称函数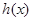 是区间D上的凹函数.设函数
是区间D上的凹函数.设函数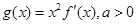 ,其中
,其中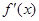 是
是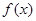 的导函数.根据上述定义,判断函数
的导函数.根据上述定义,判断函数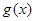 是否为其定义域内的凹函数,并说明理由.
是否为其定义域内的凹函数,并说明理由.
(本题满分13分)
已知正项数列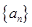 的前
的前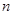 项和为
项和为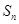 ,且满足
,且满足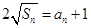 ,
,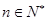 .
.
(I)求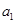 、
、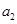 的值,并求数列
的值,并求数列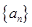 的通项公式;
的通项公式;
(II)设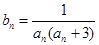 ,数列
,数列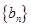 的前
的前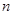 项和为
项和为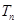 ,证明:
,证明: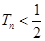 .
.
(本题满分12分)
如图,在四棱锥 中,
中, 为正三角形,
为正三角形, ⊥平面
⊥平面 ,
, ⊥平面
⊥平面 ,
, 为棱
为棱 的中点,
的中点, .
.
(I)求证: ∥平面
∥平面 ;
;
(II)求证:平面 ⊥平面
⊥平面 .
.
(本小题满分12分)为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶图如图所示:
(I)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(II)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中地理成绩;
(III)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率.