已知函数
(I)求函数 的极值;
的极值;
(II)对于函数 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数 ,使得不等式
,使得不等式 和
和 都成立,则称直线
都成立,则称直线 是函数
是函数 和
和 的“分界线”.
的“分界线”.
设函数 ,
,
 ,试问函数
,试问函数 和
和 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
已知函数 .
.
(1)当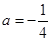 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 在区间
在区间 上是减函数,求实数a的取值范围;
上是减函数,求实数a的取值范围;
(3)当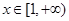 时,函数
时,函数 图象上的点都在
图象上的点都在 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
在锐角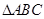 中,
中,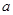 、
、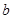 、
、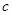 分别为角
分别为角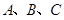 所对的边,且
所对的边,且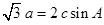 .
.
(Ⅰ)确定角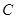 的大小;
的大小;
(Ⅱ)若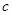 =
=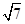 , 且
, 且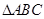 的面积为
的面积为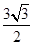
 , 求
, 求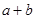 的值.
的值.
某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者从装有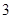 个红球、
个红球、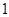 个蓝球、6个白球的袋中任意摸出4个球.根据摸出
个蓝球、6个白球的袋中任意摸出4个球.根据摸出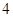 个球中红球与蓝球的个数,设一、二、三等奖如下:
个球中红球与蓝球的个数,设一、二、三等奖如下:
| 奖级 |
摸出红、蓝球个数 |
获奖金额 |
| 一等奖 |
3红1蓝 |
200元 |
| 二等奖 |
3红1白 |
50元 |
| 三等奖 |
2红1蓝或2红2白 |
10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额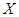 的分布列与期望
的分布列与期望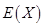 .
.
等比数列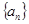 的前n项和
的前n项和 ,已知对任意的
,已知对任意的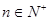 ,点
,点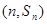 均在函数
均在函数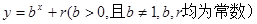 的图像上.
的图像上.
(1)求r的值.
(2)当b=2时,记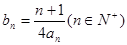 ,求数列
,求数列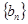 的前n项和
的前n项和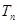 .
.
已知函数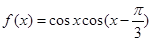
(1)求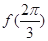 的值;
的值;
(2)求使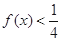 成立的
成立的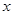 的取值集合.
的取值集合.