(本题满分13分)已知三点
（1）求以
为焦点且过点
的椭圆的标准方程；
（2）设点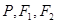
关于直线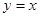
的对称点分别为
，求以
为焦点且过点
的双曲线的标准方程。
甲、乙两人在罚球线投球命中的概率分别为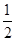
与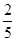
，且各次投球相互之间没有影响．
（1）甲、乙两人在罚球线各投球一次，求这二次投球中恰好命中一次的概率；
（2）甲、乙两人在罚球线各投球二次，求这四次投球中至少有一次命中的概率．
已知：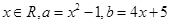
．求证：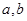
中至少有一个不小于
．
已知函数
.
（Ⅰ）当
时，求函数
在
处的切线方程；
（Ⅱ）求函数的单调区间；
（Ⅲ）若函数有两个极值点
，不等式
恒成立，求实数
的取值范围.
已知椭圆
的离心率为
，且它的一个焦点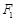
的坐标为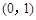
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设过焦点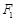的直线与椭圆相交于
两点，
是椭圆上不同于的动点，试求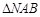
的面积的最大值.
某商场的销售部经过市场调查发现，该商场的某种商品每日的销售量
（单位：千克）与销售价格
（单位：元/千克）满足关系式
，其中
，
为常数．已知销售价格为5元/千克时，每日可售出该商品11千克．
（Ⅰ）求的值；
（Ⅱ）若该商品的成本为
元/千克，试确定销售价格的值，使该商场每日销售该商品所获得的利润最大.