已知椭圆 的离心率为
的离心率为 ,且它的一个焦点
,且它的一个焦点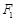 的坐标为
的坐标为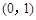 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过焦点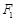 的直线与椭圆相交于
的直线与椭圆相交于 两点,
两点, 是椭圆上不同于
是椭圆上不同于 的动点,试求
的动点,试求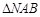 的面积的最大值.
的面积的最大值.
已知椭圆 ,且C1,C2的公共弦AB过椭圆C1的右焦点。
,且C1,C2的公共弦AB过椭圆C1的右焦点。
(1)求椭圆的焦点坐标及m=0,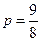 时
时 的焦点坐标;
的焦点坐标;
(2)当AB⊥x轴时,判断抛物线C2的焦点是否在直线AB上;
(3)是否存在m,p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m,p的值;若不存在,请说明理由。
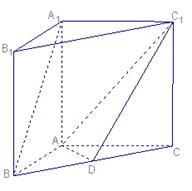
如图,在三棱柱 中,
中,  ,
, ,
, ,点D是
,点D是 上一点,且
上一点,且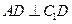 。
。
(1)求证:平面 平面
平面 ;
;
(2)求证: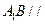 平面
平面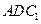 ;
;
(3)求二面角 的余弦值
的余弦值
湖南大学自主招生选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(1)求该选手被淘汰的概率;
(2)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望
设a为实数,函数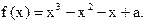
(1) 求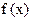 的极值及单调区间;
的极值及单调区间;
(2) 当a在什么范围内取值时, 曲线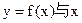 轴仅有一个交点?
轴仅有一个交点?
12月30日晚上,高二年级举行2011年元旦“师生红歌会”,某班有4名老师和4名学生站成一排。
(1)全部站成一排,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
(2)全部 站成一排,4名学生必须排在一起,共有多少种不同的排法?
站成一排,4名学生必须排在一起,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)
(3)全部站成一排,任两名学生都不能相邻,共有多少种不同的排法? (要求用数字作答)
(要求用数字作答)