在极坐标系中,圆 的极坐标方程为
的极坐标方程为 .现以极点
.现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系.
轴的非负半轴建立平面直角坐标系.
(Ⅰ)求圆 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若圆 上的动点
上的动点 的直角坐标为
的直角坐标为 ,求
,求 的最大值,并写出
的最大值,并写出 取得最大值时点P的直角坐标.
取得最大值时点P的直角坐标.
在锐角△ABC中,角A、B、C的对边分别为a、b、c,且
(1)求角 ;
;
(2)若 ,求
,求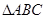 面积S的最大值.
面积S的最大值.
已知 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,且
,且 ,求
,求 的值.
的值.
已知命题:“ ,使等式
,使等式 成立”是真命题.
成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式 的解集为N,若
的解集为N,若 是
是 的必要条件,求a的取值范围.
的必要条件,求a的取值范围.
设函数 ,
, .
.
(Ⅰ)若 ,求
,求 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的结论下,是否存在实常数 和
和 ,使得
,使得 和
和 ?若存在,求出
?若存在,求出 和
和 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设 有两个零点
有两个零点 ,且
,且 成等差数列,试探究
成等差数列,试探究 值的符号.
值的符号.
设等比数列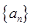 的首项为
的首项为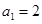 ,公比为
,公比为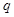 (
(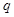 为正整数),且满足
为正整数),且满足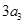 是
是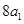 与
与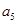 的等差中项;数列
的等差中项;数列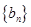 满足
满足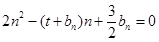 (
(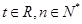 ).
).
(Ⅰ)求数列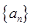 的通项公式;
的通项公式;
(Ⅱ)试确定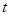 的值,使得数列
的值,使得数列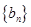 为等差数列;
为等差数列;
(Ⅲ)当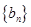 为等差数列时,对每个正整数
为等差数列时,对每个正整数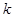 ,在
,在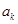 与
与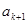 之间插入
之间插入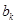 个2,得到一个新数列
个2,得到一个新数列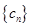 . 设
. 设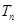 是数列
是数列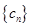 的前
的前 项和,试求满足
项和,试求满足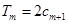 的所有正整数
的所有正整数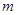 .
.