设等比数列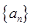 的首项为
的首项为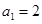 ,公比为
,公比为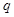 (
(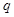 为正整数),且满足
为正整数),且满足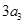 是
是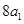 与
与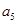 的等差中项;数列
的等差中项;数列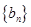 满足
满足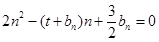 (
(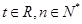 ).
).
(Ⅰ)求数列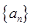 的通项公式;
的通项公式;
(Ⅱ)试确定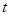 的值,使得数列
的值,使得数列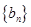 为等差数列;
为等差数列;
(Ⅲ)当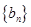 为等差数列时,对每个正整数
为等差数列时,对每个正整数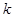 ,在
,在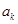 与
与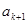 之间插入
之间插入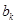 个2,得到一个新数列
个2,得到一个新数列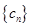 . 设
. 设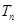 是数列
是数列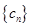 的前
的前 项和,试求满足
项和,试求满足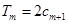 的所有正整数
的所有正整数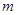 .
.
已知△ 的内角
的内角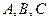 所对的边分别为
所对的边分别为 且
且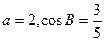 .
.
(1) 若 , 求
, 求 的值;
的值;
(2) 若△ 的面积
的面积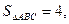 求
求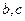 的值.
的值.
设条件p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0,若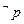 是
是 的必要不充分条件,求实数a的去值范围.
的必要不充分条件,求实数a的去值范围.
已知函数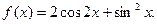
(1)求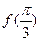 的值;
的值;
(2)求 的最大值和最小值。
的最大值和最小值。
(本题12分)
如图1所示,在平行六面体ABCD—A 1B1C1D1中,已知AB=5,AD=4,AA1=3
1B1C1D1中,已知AB=5,AD=4,AA1=3 ,AB⊥AD,∠A1AB=∠A1AD=
,AB⊥AD,∠A1AB=∠A1AD=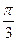 。(1)求证:顶点A1在底面ABCD上的射影O在∠BAD
。(1)求证:顶点A1在底面ABCD上的射影O在∠BAD 的平分线上;
的平分线上;
(2)求这个平行六面体的体积。
图1
(本题12分)
在单位正方体 中,M,N,
中,M,N, P分别是
P分别是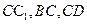 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.
( 1)求证:OM 平面
平面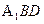 ;
;
(2)平面MNP 平面
平面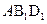 ;
;
(3)求B到平面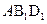 的距离
的距离