(本题12分)
在单位正方体 中,M,N,
中,M,N, P分别是
P分别是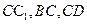 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.
( 1)求证:OM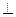 平面
平面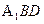 ;
;
(2)平面MNP 平面
平面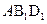 ;
;
(3)求B到平面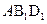 的距离
的距离
(本小题满分12分)
已知集合
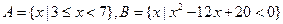 ,
, 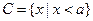 .
.
(1)求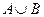 ;
;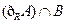
(2)若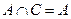 ,求
,求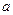 的取值范围
的取值范围
(本小题满分14分
函数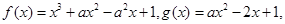 实数
实数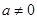 .
.
(I)若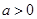 ,求函数
,求函数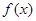 的单调区间;
的单调区间;
(II)当函数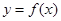 与
与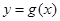 的图象只有一个公共点且
的图象只有一个公共点且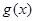 存在最小值时,记
存在最小值时,记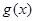 的最小值为
的最小值为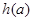 ,求的值域;
,求的值域;
(III)若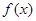 与
与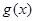 在区间
在区间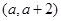 内均为增函数,求
内均为增函数,求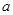 的取值范围。
的取值范围。
(文)已知函数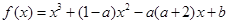
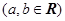 .
.
(I)若函数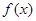 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是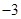 ,求
,求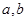 的值;
的值;
(II)若函数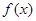 在区间
在区间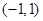 上不单调,求
上不单调,求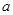 的取值范围
的取值范围
(本小题满分12分)
数列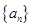 满足
满足
(1)求数列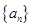 的通项公式;
的通项公式;
(2)令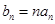 ,求数列的前n
,求数列的前n 项和
项和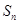
(本小题满分12分)
已知 是等比数列,
是等比数列,  ,
,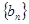 是等差数列,
是等差数列,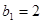
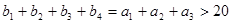
(1)求数列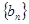 的通项公式;
的通项公式;
(2)求数列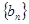 的前n项和
的前n项和 ;
;
(3)设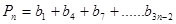 ,
, 其中n=1,2,......,试比较
其中n=1,2,......,试比较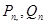 的大小。
的大小。
(本小题满分12分)
在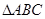 中,
中,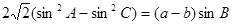 ,外接圆半径为
,外接圆半径为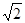 。
。
(1)求角C;
(2)求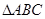 面积的最大值
面积的最大值