(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①所调查的七年级50名学生在这个月内做好事次数的平均数是 ,众数是 ,极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
(2)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球.
①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?
如图,已知直线y=-2x+4与x轴、y轴分别相交于A、C两点,抛物线y=-2x2+bx+c (a≠0)经过点A、C.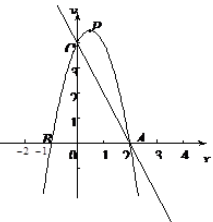
(1)求抛物线的解析式;
(2)设抛物线的顶点为P,在抛物线上存在点Q,使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;
(3)点M是直线y=-2x+4上的动点,过点M作ME垂直x轴于点E,在y轴(原点除外)上是否存在点F,使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标;若不存在,请说明理由.
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.
请按照小萍的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,求证:四边形AEGF是正方形;
(2)设AD=x,建立关于x的方程模型,求出x的值.
某超市在销售中发现:某种新年吉祥物品平均每天可售出20套,每套盈利40元。为了迎接新年,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价1元,那么平均每天就可多售出2套。要想平均每天在销售这种吉祥物上盈利1200元,那么每套应降价多少?
小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,∠ACD=45°,⊙O的半径是4cm.
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).