如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,∠ACD=45°,⊙O的半径是4cm.
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
某班同学在一次综合实践活动中,对本县居民参加“全民医保”情况进行了调查,同学们利用节假日随机调查了3000人,对调查结果进行了统计分析,绘制出两幅不完整的统计图:
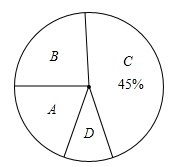
[注:图中A表示城镇职工基本医疗保险;B表示城镇居民基本医疗保险;C表示“新型农村合作医疗”;D表示其他情况]
(1)补全条形统计图;
(2)在本次调查中,B类人数占被调查人数的百分比为 ;扇形统计图中D区域所对应的圆心角的大小为 .
(3)据了解,国家对B类人员每人每年补助210元.已知该县人口数约为100万,请估计该县B类人员每年享受国家补助共多少元?
如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数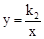 (k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.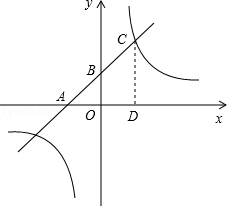
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
已知ab=﹣3,a+b=2.求代数式a3b+ab3的值.
如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程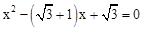 的两个根,点C在x轴负半轴上,
的两个根,点C在x轴负半轴上,
且AB:AC=1:2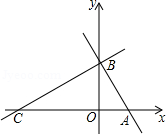
(1)求A、C两点的坐标;
(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以 A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
在国道202公路改建工程中,某路段长4000米,由甲乙两个工程队拟在30天内(含30天)合作完成,已知两个工程队各有10名工人(设甲乙两个工程队的工人全部参与生产,甲工程队每人每天的工作量相同,乙工程队每人每天的工作量相同),甲工程队1天、乙工程队2天共修路200米;甲工程队2天,乙工程队3天共修路350米.
(1)试问甲乙两个工程队每天分别修路多少米?
(2)甲乙两个工程队施工10天后,由于工作需要需从甲队抽调m人去学习新技术,总部要求在规定时间内完成,请问甲队可以抽调多少人?
(3)已知甲工程队每天的施工费用为0.6万元,乙工程队每天的施工费用为0.35万元,要使该工程的施工费用最低,甲乙两队需各做多少天?最低费用为多少?