已知 是中心在坐标原点
是中心在坐标原点 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 的离心率
的离心率 为
为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设: 、
、 为椭圆
为椭圆 上不同的点,直线
上不同的点,直线 的斜率为
的斜率为 ;
; 是满足
是满足 (
( )的点,且直线
)的点,且直线 的斜率为
的斜率为 .
.
①求 的值;
的值;
②若 的坐标为
的坐标为 ,求实数
,求实数 的取值范围.
的取值范围.
在二项式 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的常数项;
(2)求展开式中二项式系数最大的项;
(3)求展开式中各项的系数和。
△ABC的两个顶点坐标分别是B(0,6)和C(0,-6),另两边AB、AC的斜率的乘积是-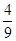 ,求顶点A的轨迹方程.
,求顶点A的轨迹方程.
已知函数
(Ⅰ)若函数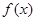 无零点,求实数
无零点,求实数 的取值范围;
的取值范围;
(Ⅱ)若函数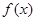 在
在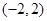 有且仅有一个零点,求实数
有且仅有一个零点,求实数 的取值范围.
的取值范围.
某商店将进货价10元的商品按每个18元出售时,每天可卖出60个.商店经理到市场做了一番调研后发现,如将这种商品的售价(在每个18元的基础上)每提高1元,则日销售量就减少5个;如将这种商品的售价(在每个18元的基础上)每降低1元,则日销售量就增加10个.为获得每日最大的利润,此商品售价应定为每个多少元?
函数 的最大值为6.求
的最大值为6.求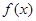 最小值.
最小值.