(本题满分12 分)
已知
(Ⅰ)将 化成
化成 的形式;
的形式;
(Ⅱ)求 的最小正周期和最大值以及取得最大值时的
的最小正周期和最大值以及取得最大值时的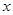 的值;
的值;
(Ⅲ)求  的单调递增区间。
的单调递增区间。
(本题满分12 分)
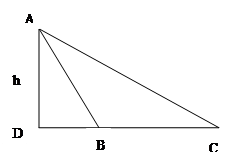
如图,从气球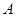 上测得正前方的河流的两岸
上测得正前方的河流的两岸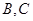 的俯角分别为
的俯角分别为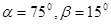 ,如果这时气球的高度
,如果这时气球的高度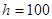 米,求河流的宽度
米,求河流的宽度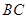 .
.
(本题满分12 分)
已知数列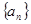 为等比数列,且首项为
为等比数列,且首项为 ,公比为
,公比为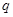 ,前
,前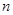 项和为
项和为 .
.
(Ⅰ)试用 ,
,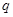 ,
,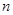 表示前
表示前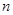 项和
项和 ;
;
(Ⅱ)证明(Ⅰ)中所写出的等比数列的前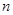 项和公式。
项和公式。
(本题满分12 分)
(1)计算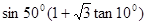 ,
,
(2)已知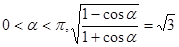 ,求sin
,求sin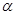 的值。
的值。
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=-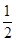 对称,且f′(1)=0.
对称,且f′(1)=0.
(1)求实数a,b的值;
(2)讨论函数f(x)的单调性,并求出单调区间 。