(本题满分12 分)
已知
(Ⅰ)将 化成
化成 的形式;
的形式;
(Ⅱ)求 的最小正周期和最大值以及取得最大值时的
的最小正周期和最大值以及取得最大值时的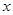 的值;
的值;
(Ⅲ)求  的单调递增区间。
的单调递增区间。
在平面直角坐标系 中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1:
中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1: ,C2:
,C2: . 设点P的轨迹为
. 设点P的轨迹为 .
.
(1)求C的方程;
(2)设直线 与C交于A,B两点.问k为何值时
与C交于A,B两点.问k为何值时

 ?此时
?此时 的值是多少?
的值是多少?
已知数列 的前
的前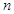 项和为
项和为 ,对一切正整数
,对一切正整数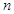 ,点
,点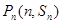 都在函数
都在函数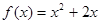 的图象上.
的图象上.
(1)求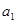 ,
, ;
;
(2)求数列 的通项公式;
的通项公式;
(3)若 ,求证数列
,求证数列 的前
的前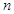 项和
项和 .
.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点, 是AC的中点,已知
是AC的中点,已知 ,
, .
.
(1)求证:OD//平面VBC;
(2)求证:AC⊥平面VOD;
(3)求棱锥 的体积.
的体积.
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
在DABC中,角A、B、C的对边分别为a、b、c,且角A、B都是锐角,a=6,b=5, .
.
(1) 求 和
和 的值;
的值;
(2) 设函数 ,求
,求 的值.
的值.