定义首项为1且公比为正数的等比数列为"M－数列".
（1）已知等比数列{ a n} 满足： ，求证:数列{ a n}为"M－数列"；
（2）已知数列{ b n}满足: ，其中 S n为数列{ b n}的前 n项和．
①求数列{ b n}的通项公式；
②设 m为正整数，若存在"M－数列"{ c n} ，对任意正整数 k ，当 k≤ m时，都有 成立，求 m的最大值．
设数列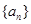
是等比数列，
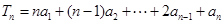，已知
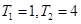, (1)求数列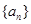的首项和公比；（2）求数列
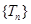的通项公式。
某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量（单位：吨） |
2 |
3 |
4 |
| 频数 |
20 |
50 |
30 |
⑴ 根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵ 已知每吨该商品的销售利润为2千元,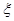
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求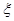的分布列和数学期望.
已知集合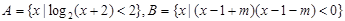
，若
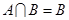，求实数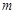
的取值范围.
利用幂函数图象，画出下列函数的图象（写清步骤）.
（1）
．
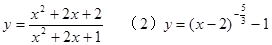由于对某种商品开始收税，使其定价比原定价上涨x成（即上涨率为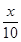
），涨价后，商品卖出个数减少bx成，税率是新定价的a成，这里a,b均为正常数，且a<10，设售货款扣除税款后，剩余y元，要使y最大，求x的值.