(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,
 ,
,
(1)求证:CD ;
;
(2)求AD与SB所成角的余弦值;
(3)求二面角A—SB—D的余弦值.
(本题满分12分)在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(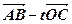 )·
)·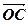 =0,求t的值。
=0,求t的值。
(本题满分12分)已知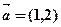 ,
, ,分别求当
,分别求当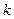 为何值时
为何值时
(1) 与
与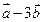 垂直?
垂直?
(2)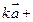
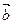 与
与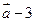
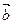 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(3)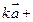
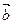 与
与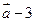
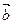 的夹角是钝角?
的夹角是钝角?
(本题满分10分)设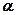 是第二象限的角,
是第二象限的角,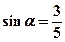 ,求
,求 的值.
的值.
(本小题满分15分)如图所示,已知椭圆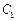 和抛物线
和抛物线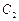 有公共焦点
有公共焦点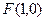 ,
, 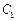 的中心和
的中心和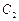 的顶点都在坐标原点,过点
的顶点都在坐标原点,过点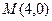 的直线
的直线 与抛物线
与抛物线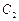 分别相交于
分别相交于 两点
两点
(1)写出抛物线
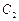 的标准方程;
的标准方程;
(2)若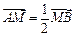 ,求直线
,求直线 的方程;
的方程;
(3)若坐标 原点
原点 关于直线
关于直线 的对称点
的对称点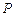 在抛物线
在抛物线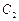 上,直线
上,直线 与椭圆
与椭圆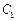 有公共点,求椭圆
有公共点,求椭圆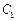 的长轴长的最小值。
的长轴长的最小值。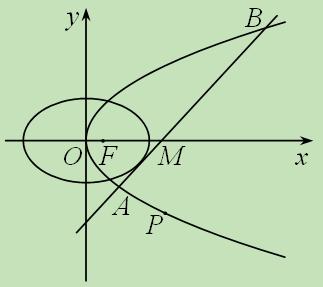
(本小题满分15分)
已知函数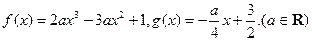
(I)当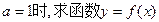 的单调区间;
的单调区间;
(II)若任意给定的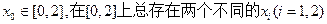 ,使得
,使得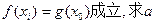 的取值范围。
的取值范围。