(本小题满分15分)如图所示,已知椭圆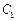 和抛物线
和抛物线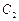 有公共焦点
有公共焦点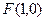 ,
, 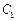 的中心和
的中心和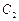 的顶点都在坐标原点,过点
的顶点都在坐标原点,过点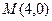 的直线
的直线 与抛物线
与抛物线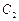 分别相交于
分别相交于 两点
两点
(1)写出抛物线
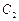 的标准方程;
的标准方程;
(2)若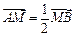 ,求直线
,求直线 的方程;
的方程;
(3)若坐标 原点
原点 关于直线
关于直线 的对称点
的对称点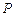 在抛物线
在抛物线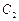 上,直线
上,直线 与椭圆
与椭圆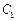 有公共点,求椭圆
有公共点,求椭圆 的长轴长的最小值。
的长轴长的最小值。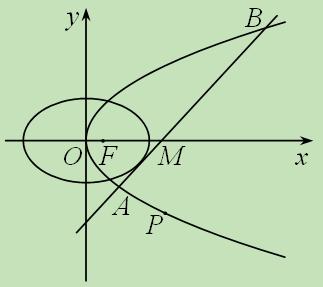
教育局派5名调研员到3所学校去调研学生作业负担问题,每校至少1人,有多少种不同的派遣方法?
用0,1,2,3,4,5共6个数字,可以组成多少个没有重复数字的6位奇数?
有A,B,C三个城市,上午从A城去B城有5班汽车,2班火车,都能在12:00前到达B城,下午从B城去C城有3班汽车,2班轮船.某人上午从A城出发去B城,要求12:00前到达,然后他下午去C城,问有多少种不同的走法?
设 是定义在
是定义在 上的函数,且
上的函数,且 .
.
(1)若 ,求
,求 ;
;
(2)若 ,求
,求 .
.
从射击、乒乓球、跳水、田径四个大项的雅典奥运冠军中选出10名作“夺冠之路”的励志报告.
(1)若每个大项中至少选派两人,则名额分配有几种情况?
(2)若将10名冠军分配到11个院校中的9个院校作报告,每个院校至少一名冠军,则有多少种不同的分配方法?