教育局派5名调研员到3所学校去调研学生作业负担问题,每校至少1人,有多少种不同的派遣方法?
已知函数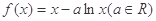
(1)当a=2时,求曲线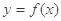 在点A(1,f(1))处的切线方程;
在点A(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性与极值.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.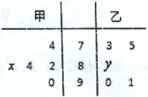
(1)求出x,y的值,且分别求甲、乙两个班中5名学生成绩的方差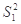 、
、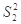 ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
等差数列{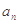 }足:
}足: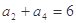 ,
,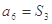 ,其中
,其中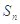 为数列{
为数列{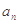 }前n项和.
}前n项和.
(1)求数列{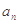 }通项公式;
}通项公式;
(2)若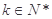 ,且
,且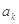 ,
, ,
,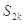 成等比数列,求k值.
成等比数列,求k值.
已知函数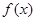 满足对任意实数
满足对任意实数 都有
都有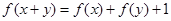 成立,且当
成立,且当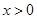 时,
时,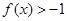 ,
,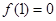 .
.
(1)求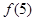 的值;
的值;
(2)判断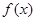 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数 ,总能找到一个正实数
,总能找到一个正实数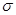 ,使得当
,使得当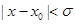 时,
时, ,则称函数
,则称函数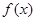 在
在 处连续。试证明:
处连续。试证明: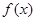 在
在 处连续.
处连续.
已知函数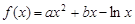 ,
,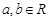 .
.
(1)若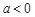 且
且 ,试讨论
,试讨论 的单调性;
的单调性;
(2)若对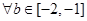 ,总
,总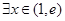 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.