(本题12分)已知抛物线y=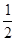
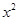 +c与x轴交于A(-1,0),B两点,交y轴于点C
+c与x轴交于A(-1,0),B两点,交y轴于点C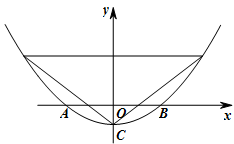
(1)求抛物线的解析式
(2)点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究)
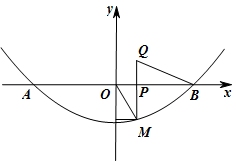
(3)如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长
(本题10分)如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q.记△AEF的面积为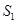 ,四边形EFQP的面积为
,四边形EFQP的面积为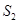 ,四边形PQCB的面积为
,四边形PQCB的面积为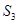
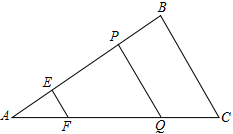
(1)求证:EF+PQ=BC
(2)若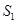 +
+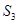 =
=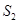 ,求
,求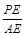 的值
的值
(3)若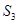 -
-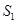 =
=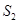 ,直接写出
,直接写出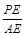 的值
的值
(本题8分)已知锐角△ABC中,边BC长为12,高AD长为8
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K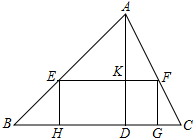
①求 的值
的值
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值
(2)若ABAC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
(本题8分)如图,AB是⊙O的直径,∠ABT=45°,AT=AB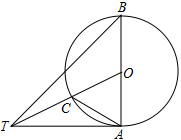
(1)求证:AT是⊙O的切线
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC的值
(本题8分),如图,已知点A(-4,2)B(-1,-2),□ABCD的对角线交于坐标原点O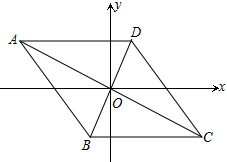
(1)请直接写出点C、D的坐标
(2)写出从线段AB到线段CD的变换过程
(3)直接写出□ABCD的面积