如图,已知点A(0,4),B(2,0).
(1)求直线AB的函数解析式;
(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.
①求线段AC的长;(用含m的式子表示)
②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.
如图,等腰梯形ABCD中,AD∥BC,点E是AD延长线上的一点,且CE=CD,求证:∠B=∠E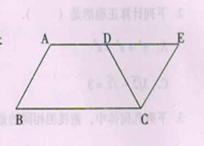
在一个口袋中有4个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求下列事件的概率:
(1)两次取的小球的标号相同
(2)两次取的小球的标号的和等于4
计算: +
+
如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OF•DE=OE•2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)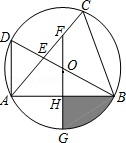
如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.