如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A、B、C三点,已知点A(﹣3,0),B(0,3),C(1,0).
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.
①动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以AP为边作图示一侧的正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.(结果保留根号)
如图,直线 为常数, 与双曲线 为常数, 的交点为 、 , 轴于点 , , .
(1)求 的值;
(2)点 在 轴上,如果 ,求 点的坐标.

已知关于 的一元二次方程
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为 、 ,且 ,求 的值.
如图, , ,垂足分别是点 、 , , ,求证: .

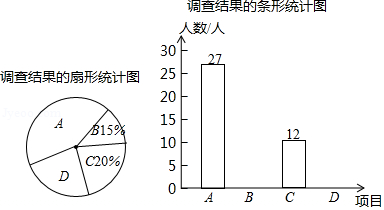
在“弘扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“ 国学诵读”、“ 演讲”、“ 课本剧”、“ 书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动 占 ,希望参加活动 占 ,则被调查的总人数为 人,扇形统计图中,希望参加活动 所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动 有多少人?
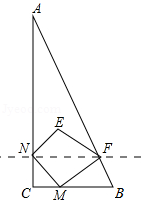
如图,已知 中, ,点 从点 出发沿 方向以 的速度匀速运动,到达点 停止运动,在点 的运动过程中,过点 作直线 交 于点 ,且保持 ,再过点 作 的垂线交 于点 ,连接 .将 关于直线 对称后得到 ,已知 , ,设点 运动时间为 , 与 重叠部分的面积为 .
(1)在点 的运动过程中,能否使得四边形 为正方形?如果能,求出相应的 值;如果不能,说明理由;
(2)求 关于 的函数解析式及相应 的取值范围;
(3)当 取最大值时,求 的值.