如图，已知函数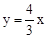
与反比例函数
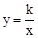（x＞0）的图象交于点A．将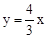的图象向下平移6个单位后与双曲线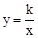交于点B，与x轴交于点C．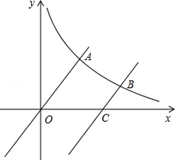
（1）求点C的坐标；
（2）若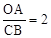
，求反比例函数的解析式．
已知抛物线经过点
(0 ，5)和 点(–1 ，0)，且对称轴为
，求函数解析式.
已知：在Rt△ABC中，∠C=90°，
,
，解这个直角三角形.
已知抛物线
用配方法求出它的顶点坐标、对称轴.
．抛物线
与
轴交于A,B两点，与
轴交于C点，且A(
,0)。
（1）求抛物线的解析式及顶点坐标D的坐标；
（2）判断
的形状，证明你的结论；（3）点M（m,0）是
轴上的一个动点，当MC+MD的值最小时，求m的值。
．某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？