我市某中学艺术节期间，向学校学生征集书画作品．九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班，对征集到的作品的数量进行了解析统计，制作了如下两幅不完整的统计图．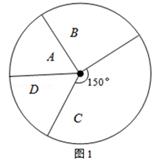
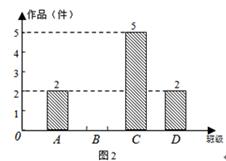
（1）李老师采取的调查方式是 （填“普查”或“抽样调查”），李老师所调查的4个班征集到作品共
件，其中B班征集到作品 ，请把图2补充完整．
（2）如果全年级参展作品中有4件获得一等奖，其中有2名作者是男生，2名作者是女生．现在要在抽两人去参加学校总结表彰座谈会，求恰好抽中一男一女的概率．（要求用树状图或列表法写出解析过程）
；
≤
，并将它的解集在数轴上表示出来.
；
）÷
.
，再将x取一个喜欢的值代入计算．