两根平行金属导轨固定倾斜放置,与水平面夹角为37°,相距d="0.5" m,a、b间接一个电阻R,R="1.5" Ω.在导轨上c、d两点处放一根质量m=0.05 kg的金属棒,bc长L="1" m,金属棒与导轨间的动摩擦因数μ=0.5.金属棒在导轨间的电阻r="0.5" Ω,金属棒被两个垂直于导轨的木桩顶住而不会下滑,如图所示.在金属导轨区域加一个垂直导轨斜向下的匀强磁场,磁场随时间的变化关系如图所示,重力加速度g=" 10" m/s2.可认为最大静摩擦力与滑动摩擦力相等,(sin37°=0.6,cos 37° =0.8).求: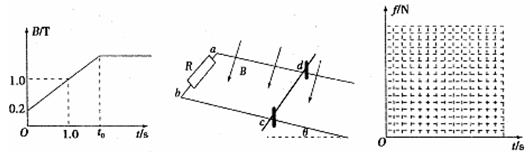
(1)0~1.0 s内回路中产生的感应电动势大小;
(2)t=0时刻,金属棒所受的安培力大小;
(3)在磁场变化的全过程中,若金属棒始终没有离开木桩而上滑,则图4中t0的最大值;
(4)通过计算在图6中画出0~t0max内金属棒受到的静摩擦力随时间的变化图象.
一个静止的质量为m1的铀核 ,放出
,放出 一个质量为m2的α粒子后,衰变成质量为m3的钍核
一个质量为m2的α粒子后,衰变成质量为m3的钍核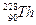 。(已知光速为c)
。(已知光速为c)
(1)写出核衰变反应方程
(2)算出该核衰变反应中释放出的核能
(3)假设反应中释放出的核能全部转化为钍核和α粒子的动能,则钍核获得的动能有多大(用字母m1、m2、m3、c表示结果)
如图所示,平板B的质量为mB=1kg,放置在光滑的水平面上,质量为mA=2kg的小铁块A,以vA="2" m/s的速度水平向右滑上平板,小铁块A最终没有滑离平板B,取水平向右为正方向,小铁块A看成质点,求:
(1)如图甲所示,若平板B开始静止,平板B的最终速度的大小和方向
(2)如图乙所示,若平板B开始时是以vB=10m/s的速度向左匀速运动,平板B的最终速度大小和方向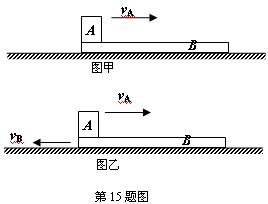
甲、乙两辆小车质量分别为m1=50kg和m2=30kg,质量m=30kg的小孩站在甲车上。两车在光滑轨道上相向运动,车速V1=3m/s,V2=4m/s,为避免两车相撞,小孩至少以多大的水平速度(相对地面)跳到乙车上?
如图所示,某透明液体深1m,一束与水平面成30o角的光线从真空照向该液体,进入该液体的光线与水平面的夹角为45o。试求:(真空的光速c≈3.0×108m/s)
(1)该液体的折射率;
(2)进入液面的光线经多长时间可以照到底面。
如图所示,在地面上方足够高的地方,存在一个高度d=0.3m的“匀强电场区域”(下图中划有虚线的部分),电场方向竖直向上,电场强度E="2mg/q" 。一个电荷量为q的带正电的小圆环A套在一根均匀直杆B上,A和B的质量均为m。开始时A处于B的最下端,B竖直放置,A距“匀强电场区域”的高度h=0.2m。让A和B一起从静止开始下落,它们之间的滑动摩擦力f=0.5mg。不计空气阻力,取重力加速度g=10m/s2。求:
(1)圆环A通过“匀强电场区域”所用的时间?
(2)假如直杆B着地前A和B的速度相同,求这一速度?
(设杆 B在下落过程中始终保持竖直且足够长)