（本小题满分12分）
某学校高二年级共有1000名学生，其中男生650人，女生350人，为了调查学生周末的休闲方式，用分层抽样的方法抽查了200名学生.
（1）完成下面的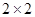
列联表；
| |
不喜欢运动 |
喜欢运动 |
合计 |
| 女生 |
50 |
|
|
| 男生 |
|
|
|
| 合计 |
|
100 |
200 |
（2）在喜欢运动的女生中调查她们的运动时间， 发现她们的运动时间介于30分钟到90分钟之间，如图是测量结果的频率分布直方图，若从区间段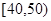
和
的所有女生中随机抽取两名女生，求她们的运动时间在同一区间段的概率.
中，
，求数列
的前
项和
．
是等比数列，且
，
的表达式；
．
中，角
对应边分别为
，且
的大小；
；（2）证明：
．
在区间
上任取两个实数
与
可以构成钝角三角形三边长的概率。