阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp﹣x1=x2﹣xp,得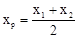 ,同理
,同理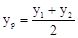 ,所以AB的中点坐标为
,所以AB的中点坐标为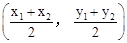 .由勾股定理得
.由勾股定理得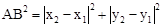 ,所以A、B两点间的距离公式为
,所以A、B两点间的距离公式为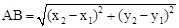 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.
解答下列问题: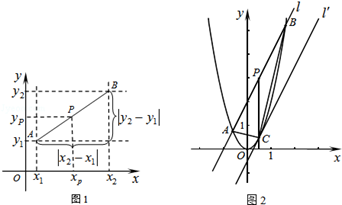
如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(1)求A、B两点的坐标及C点的坐标;
(2)连结AB、AC,求证△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
供电局的电力维修工甲、乙两人要到45千米远的A地进行电力抢修.甲骑摩托车先行,t(t≥0)小时后乙开抢修车载着所需材料出发.若
 (小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;
(小时),抢修车的速度是摩托车的1.5倍,且甲、乙两人同时到达,求摩托车的速度;若摩托车的速度是45千米/小时,抢修车的速度是60千米/小时,且乙不能比甲晚到,则t的最大值是多少?
如图,在平面直角坐标系中,直线 分别交
分别交 轴、
轴、 轴于
轴于 两点.点
两点.点 、
、 ,以
,以 为一边在
为一边在 轴上方作矩形
轴上方作矩形 ,且
,且 .设矩形
.设矩形 与
与 重叠部分的面积为
重叠部分的面积为 .
.求点
 、
、 的坐标;
的坐标;当
 值由小到大变化时,求
值由小到大变化时,求 与
与 的函数关系式;
的函数关系式;若在直线
 上存在点
上存在点 ,使
,使 等于
等于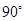 ,请直接写出
,请直接写出 的取值范围.
的取值范围.
如图1,在 中,
中, 为锐角,点
为锐角,点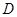 为射线
为射线 上一点,联结
上一点,联结 ,以
,以 为一边且在
为一边且在 的右侧作正方形
的右侧作正方形 .
.如果
 ,
, ,
,
①当点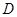 在线段
在线段 上时(与点
上时(与点 不重合),如图2,线段
不重合),如图2,线段 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段 的数量关系为 ;
的数量关系为 ;
②当点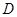 在线段
在线段 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;如果
 ,
, 是锐角,点
是锐角,点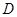 在线段
在线段 上,当
上,当 满足什么条件时,
满足什么条件时, (点
(点 不重合),并说明理由.
不重合),并说明理由.
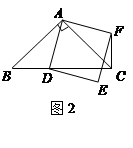

如图1,矩形纸片ABCD中,AB=4,BC=4 ,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
已知:如图,AB∥DE,∠A=∠D,且BE=CF,求证:∠ACB=∠F.