如图(1),在Rt△ABC, ∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M。
(1)求证:△ABD≌△FBC;
(2)如图(2),已知AD=6,求四边形AFDC的面积;
(3)在△ABC中,设BC=a,AC=b,AB=c,当∠ACB≠90°时,c2≠a2+b2。在任意△ABC中,c2=a2+b2+k。就a=3,b=2的情形,探究k的取值范围(只需写出你得到的结论即可)。
解方程(每题4分)
因式分解:(每题3分,共9分)
(1) ;
;
(2) ;
;
(3) .
.
秋交会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?(利润=销售总价-成本总价)
(3)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
阅读材料:
例:说明代数式 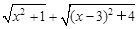 的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
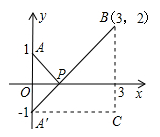
解: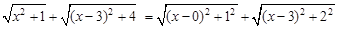 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则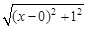 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离,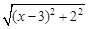 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B= ,即原式的最小值为
,即原式的最小值为 .
.
根据以上阅读材料,解答下列问题:
(1)代数式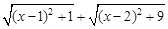 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B的距离之和.(填写点B的坐标)
(2)代数式 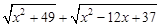 的最小值.
的最小值.
(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BF=AE.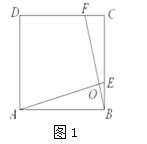
(2) 如图2,正方形ABCD边长为12,将正方形沿MN折叠,使点A落在DC边上的点E处,且DE=5,求折痕MN的长.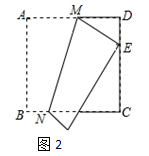
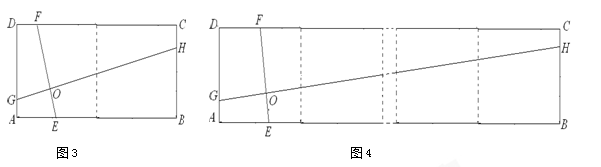
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4.直接写出下列两题的答案:①如图3,矩形ABCD由2个全等的正方形组成,则 GH=___________;
②如图4,矩形ABCD由n个全等的正方形组成,则 GH=___________;(用n的代数式表示).