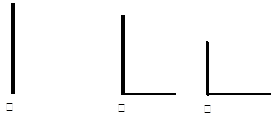如图1，平面之间坐标系中，等腰直角三角形的直角边BC在x轴正半轴上滑动，点C的坐标为（t，0），直角边AC=4，经过O，C两点做抛物线
（a为常数，a＞0），该抛物线与斜边AB交于点E，直线OA：y2=kx（k为常数，k＞0）
（1）填空：用含t的代数式表示点A的坐标及k的值：A ，k= ；
（2）随着三角板的滑动，当a=
时：
①请你验证：抛物线的顶点在函数
的图象上；
②当三角板滑至点E为AB的中点时，求t的值；
（3）直线OA与抛物线的另一个交点为点D，当t≤x≤t+4，|y2﹣y1|的值随x的增大而减小，当x≥t+4时，|y2﹣y1|的值随x的增大而增大，求a与t的关系式及t的取值范围．
一个直棱柱的三视图如图，用文字描述这个直棱柱的形状，并求出这个直棱柱的表面积．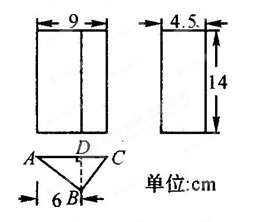
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：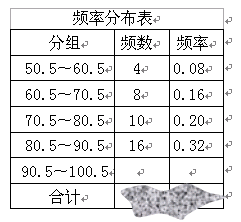
填充频率分布表中的空格；
补全频率分布直方图
在该问题中的样本容量是多少？
答：．全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）
答：．若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
答：．
在湖的两岸A、B间建一座观赏桥，由于条件限制，无法直接度量A、B两点间的距离。请你用学过的数学知识按以下要求设计一测量方案。画出测量图案
写出测量步骤（测量数据用字母表示）
计算AB的距离（写出求解或推理过程，结果用字母表示）。
如图，Rt△ABO的顶点A是双曲线
与直线
在第二象限的交点，AB⊥
轴于B且S△ABO=
求这两个函数的解析式
求直线与双曲线的两个交点A，C的坐标和△AOC的面积。
三根垂直地面的木杆甲、乙、丙，在路灯下乙、丙的影子如图所示。试确定路灯灯炮的位置，再作出甲的影子。（不写作法，保留作图痕迹）