如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，二次函数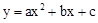
的图象经过点A，B，与x轴分别交于点E，F，且点E的坐标为（
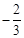，0），以OC为直径作半圆，圆心为D．
（1）求二次函数的解析式；
（2）求证：直线BE是⊙D的切线；
（3）若直线BE与抛物线的对称轴交点为P，M是线段CB上的一个动点（点M与点B，C不重合），过点M作MN∥BE交x轴与点N，连结PM，PN，设CM的长为t，△PMN的面积为S，求S与t的函数关系式，并写出自变量t的取值范围．S是否存在着最大值？若存在，求出最大值；若不存在，请说明理由．
如图,点A坐标为(－1,1),将此小船向左平移2个单位后,画出图形,并指出A,B,C,D各点坐标.
夏令营组织学员到某一景区游玩，老师交给同学一张画有直角坐标系和标有A、B、C、D 四个景点位置的地图，指出：今天我们游玩的景点E是新开发的，地图上还没来得及标注，但已知这个景点E满足：①与景点A、C和景点B、D所在的两条直线等距离；②到B、C两景点等距离。请你在平面直角坐标系中，画出景点E的位置，并标明坐标（用整数表示）。 
如图，在直角坐
标系中，已知点P0的坐标
为(1，0)，将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此
下去，得到线段OP3，OP4，…，OPn(n为正整数)
(1)求点P6的坐标；
(2)求△P5OP6的面积；
(3)我们规定：把点Pn(xn，yn)(n=0，1，2，3…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|，|yn|)称之为点Pn的“绝对坐标”．根据图中点Pn的分布规律，请你猜想点Pn的“绝对坐标”，并写出来
随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加.据统计，某小区2006年底拥有家庭轿车64辆，2008年底家庭轿车的拥有量
达到100辆.
（1）若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同，求该小区到2009年底家庭轿车将达到多少
辆？
（2）为了缓解停车矛盾，该小区决定投资15万元再建造若干个停车位.据测算，建造费用分别为室内车位5000元/个，露天车位1000元/个，考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，求该小区最多可建两
种车位各多少个？试写出所有可能的方案
已知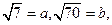
用含的
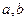代数式表示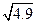
.甲、乙两位同学跑上讲台，板书了下面两种解法：
同学甲解：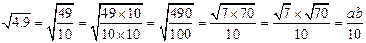 
同学乙解：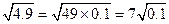
因为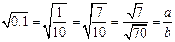
， 
.
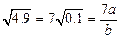老师看罢，提出下面的问题：
（1）两位同学的解法都正确吗？为什么？
（2）请你再给出一种不同于甲、乙二人的解法