如图，直线
与⊙O相切于点D，过圆心O作EF∥交⊙O于E、F两点，点A是⊙O上一点，连接AE，AF，并分别延长交直线于B、C两点；
（1）求证：∠ABC+∠ACB=90°；
（2）若⊙O的半径
，BD=12，求tan∠ACB的值．
如图，在梯形纸片ABCD中，BC∥AD,∠A+∠D=90°,tanA=2，过点B作BH⊥AD与H,BC=BH=2.动点
从点
出发，以每秒1个单位的速度沿
运动到点
停止，在运动过程中，过点作
交折线
于点
，将纸片沿直线
折叠，点
、的对应点分别是点
、
。设点运动的时间是
秒（
）。
（1）当点和点重合时，求运动时间的值；
（2）在整个运动过程中，设
或四边形
与梯形
重叠部分面积为
，请直接写出与之间的函数关系式和相应自变量的取值范围；
（3）平移线段
，交线段
于点
，交线段
。在直线
上存在点
，使
为等腰直角三角形。请求出线段
的所有可能的长度。
在平面直角坐标系中，△ABC的位置如图所示，请解答下列问题：
（1）将△ABC向下平移3个单位长度，得到△A1B1C1，画出平移后的△A1B1C1；
（2）将△ABC绕点O顺时针方向旋转180°，得到△A2B2C2，画出旋转后的△A2B2C2，并写出A2点的坐标．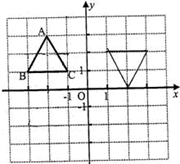
某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元．在销售过程中发现，年销售量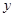
（万件）与销售单位
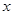（元）之间存在着如图所示的一次函数关系．
（1）求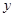关于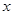的函数关系式；
（2）试写出该公司销售该种产品的年获利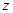
（万元）关于销售单价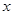（元）的函数关系式（年获利＝年销售额－年销售产品总进价－年总开支）．当销售单价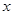为何值时，年获利最大？并求这个最大值；
（3）若公司希望该种产品一年的销售获利不低于40万元，借助（2）中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？
当a=－3，b=－2，c=5时，求下列各代数式的值。
（1）a÷bc(即a÷(bc))；
（2）ab÷c；
（3）
；
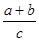（4）
；
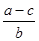（5）
；
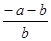（6）
；
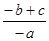某包装盒的展开图，尺寸如图所示（单位：cm）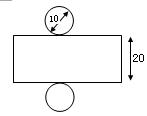
（1）这个几何体的名称是；
（2）求这个包装盒的表面积