已知，如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD。以AD为斜边在平行四边形ABCD的内部作Rt△AED，∠EAD=300，∠AED=900。
（1）求△AED的周长；
（2）若△AED以每秒2个长度单位的速度沿DC向右平行移动，得到△A0E0D0，当A0D0与BC重合时停止移动。设移动时间为t秒，△A0E0D0与△BDC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出t的取值范围；
（3）如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转
，在旋转过程中，B的对应点为B1，E的对应点为E1，设直线B1E1与直线BE交于点P、与直线CB交于点Q。是否存在这样的
，使△BPQ为等腰三角形？若存在，求出的度数；若不存在，请说明理由。
两幢垂直于地面的大楼相距110米，从甲楼顶部看乙楼顶部的仰角为30°，已知甲楼高35米根据题意，在图中画出示意图；
求乙楼的高度为多少米？
“戒烟一小时，健康亿人行”．今年国际无烟日，小华就公众对在餐厅吸烟的态度进行了随机抽样调查，主要有四种态度：A．顾客出面制止；B．劝说进吸烟室；C．餐厅老板出面制止；D．无所谓．他将调查结果绘制了两幅不完整的统计图．请你根据图中的信息回答下列问题：
求这次抽样的公众有多少人？
请将统计图①补充完整
在统计图②中，求“无所谓”部分所对应的圆心角是多少度？
若城区人口有20万人，估计赞成“餐厅老板出面制止”的有多少万人？
小华在城区中心地带随机对路人进行调查，请你根据以上信息，求赞成“餐厅老板出面制止”的概率是多少？
计算
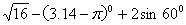．画出函数y=-x2+1的图象
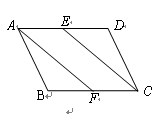
已知：如图，E，F分别是□ABCD的边AD，BC的中点．求证：AF=CE．
如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AB＝6，RtA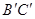
可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的，则线段
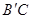的长为_________________．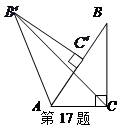
（1）如图，已知线段AB，请用直尺和圆规作出线段AB的垂直平分线（不写画法，保留作图痕迹）；
（2）计算：
（3）如图，已知 
直线
交
于
,交
于
,
平分
,
平分
求证：
