已知点P是∠MON的平分线上的一动点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.
(1)利用图1,求证:PA=PB;
(2)如图2,若点 是
是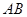 与
与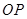 的交点,当
的交点,当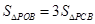 时,求PC与PB的比值;
时,求PC与PB的比值;
(3)若∠MON=60°,OB=2,射线AP交ON于点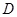 ,且满足且
,且满足且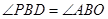 ,请借助图3补全图形,并求
,请借助图3补全图形,并求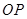 的长.
的长.
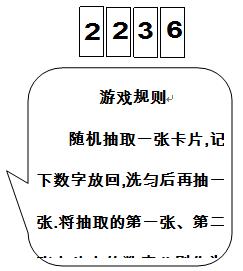
四张质地相同的卡片如图所示. 将卡片洗匀后,背面朝上放置在桌面上.求随机抽取一张卡片,恰好得到数字2的概率;
小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平.
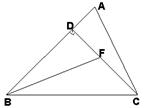
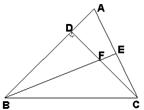
如图,已知在等腰直角三角形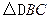 中,
中,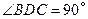 ,
, 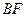 平分
平分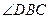 ,与
,与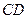 相交于点
相交于点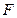 ,延长
,延长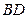 到
到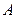 ,使
,使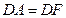 ,
,求证:
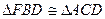
延长
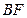 交
交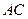 于
于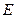 ,且
,且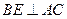 ,求证:
,求证: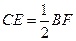
在⑵的条件下,
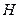 是
是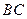 边的中点,连结
边的中点,连结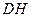 与
与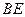 相交于点
相交于点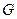 .
.
试探索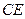 ,
,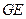 ,
,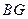 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多 少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
1 号 号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
89 |
100 |
95 |
119 |
97 |
500 |
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题计算两个班这五名学生的优秀率。
计算两个班这五名学生比赛数据的方差哪一个小
通过上面的计算你认为应该定哪一个班为冠军更合适?请你说明你的理由
如图,△ABC中,AB=AC,E,D分别是AB,AC上的点,连接BD,CE.请你增加一个条件(不再添加其它线段,不再标注其它字母),使BD=CE,并加以证明.
你添加的条件是:________________________________.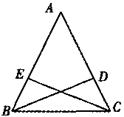
某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.符合题意的组建方案有几种?请你帮学校设计出来
若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,
试说明(1)中哪种方案费用最低,最低费用是多少元?