某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多 少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
| |
1 号 号 |
2号 |
3号 |
4号 |
5号 |
总分 |
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
89 |
100 |
95 |
119 |
97 |
500 |
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题计算两个班这五名学生的优秀率。
计算两个班这五名学生比赛数据的方差哪一个小
通过上面的计算你认为应该定哪一个班为冠军更合适?请你说明你的理由
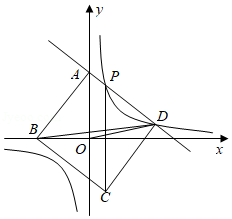
如图,一次函数 的图象与 轴的正半轴交于点 ,与反比例函数 的图象交于 , 两点.以 为边作正方形 ,点 落在 轴的负半轴上,已知 的面积与 的面积之比为 .
(1)求一次函数 的表达式;
(2)求点 的坐标及 外接圆半径的长.
某校要从甲,乙两名学生中挑选一名学生参加数学竞赛,在最近的8次选拔赛中,他们的成绩(成绩均为整数,单位:分)如下:
甲:92,95,96,88,92,98,99,100
乙:100,87,92,93,9■,95,97,98
由于保存不当,学生乙有一次成绩的个位数字模糊不清,
(1)求甲成绩的平均数和中位数;
(2)求事件“甲成绩的平均数大于乙成绩的平均数”的概率;
(3)当甲成绩的平均数与乙成绩的平均数相等时,请用方差大小说明应选哪个学生参加数学竞赛.
如图,在平行四边形 中, ,点 为线段 的三等分点(靠近点 ,点 为线段 的三等分点(靠近点 ,且 .将 沿 对折, 边与 边交于点 ,且 .
(1)证明:四边形 为矩形;
(2)求四边形 的面积.

如图①是甲,乙两个圆柱形水槽的横截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间 之间的关系如图②所示,根据图象解答下列问题:
(1)图②中折线 表示 槽中水的深度与注入时间之间的关系;线段 表示 槽中水的深度与注入时间之间的关系;铁块的高度为 .
(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)

小明在 点测得 点在 点的北偏西 方向,并由 点向南偏西 方向行走到达 点测得 点在 点的北偏西 方向,继续向正西方向行走 后到达 点,测得 点在 点的北偏东 方向,求 , 两点之间的距离.(结果保留 .参数数据
