如图①是甲,乙两个圆柱形水槽的横截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间 之间的关系如图②所示,根据图象解答下列问题:
(1)图②中折线 表示 槽中水的深度与注入时间之间的关系;线段 表示 槽中水的深度与注入时间之间的关系;铁块的高度为 .
(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)

有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元.依此类推,即每多买一台则所买各台单价均再减20元,但最低不能低于每台440元;乙公司一律按原售价的75%促销.某单位需购买一批图形计算器:
(1)若此单位需购买12台图形计算器,应去哪家公司购买花费较少?
(2)若此单位恰好花费7280元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.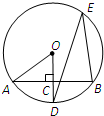
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
如图,粮仓的顶部是圆锥形,这个圆锥的底面周长为32cm,母线长为7cm,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是多少?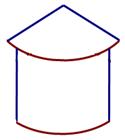
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.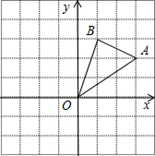
(1)画出旋转后的图形;
(2)点A1的坐标为;
(3)在旋转过程中,点B经过的路径为弧BB1,那么弧BB1的长为多少?
已知关于x的方程x2+kx-2=0的一个解与方程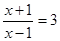 解相同.
解相同.
(1)求k的值;(2)求方程x2+kx-2=0的另一个根.