如图,四棱锥 的底面为矩形,
的底面为矩形, ,
, ,
, 分别是
分别是 的中点,
的中点, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 .
.
在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=9.
(1)判断两圆的位置关系;
(2)求直线m的方程,使直线m被圆C1截得的弦长为4,与圆C 截得的弦长是6.
截得的弦长是6.
已知点 和
和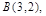 求过点
求过点 且与
且与 的距离相等的直线方程.
的距离相等的直线方程.
已知函数
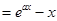 ,其中
,其中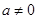 .
.
(1)若对一切x∈R, ≥1恒成立,求a的取值集合;
≥1恒成立,求a的取值集合;
(2)在函数 的图像上取定两点
的图像上取定两点 ,
,
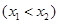 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使 成立?若存在,求
成立?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数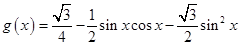 ,将其图象向左移
,将其图象向左移 个单位,并向上移
个单位,并向上移 个单位,得到函数
个单位,得到函数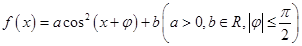 的图象.
的图象.
(1)求实数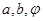 的值;
的值;
(2)设函数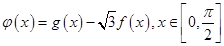 ,求函数
,求函数 的单调递增区间和最值.
的单调递增区间和最值.
已知函数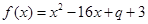 :
:
(1)若函数在区间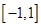 上存在零点,求实数
上存在零点,求实数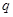 的取值范围;
的取值范围;
(2)问:是否存在常数 ,当
,当 时,
时,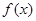 的值域为区间
的值域为区间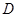 ,且
,且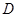 的长度为
的长度为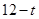 .
.