已知抛物线抛物线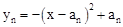 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
①若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.
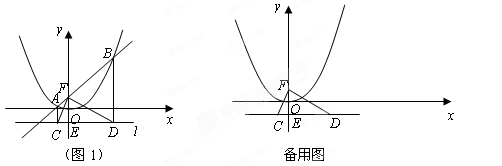
(本题10分)已知,如图,过点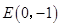 作平行于
作平行于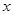 轴的直线
轴的直线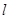 ,抛物线
,抛物线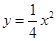 上的两点
上的两点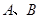 的横坐标分别为
的横坐标分别为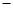 1和4,直线
1和4,直线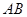 交
交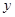 轴于点
轴于点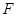 ,过点
,过点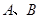 分别作直线
分别作直线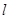 的垂线,垂足分别为点
的垂线,垂足分别为点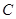 、
、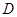 ,连接
,连接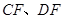 .
.
(1)求点
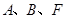 的坐标;
的坐标;(2)求证:
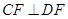 ;
;(3)点
 是抛物线
是抛物线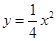 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点 作
作 交
交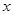 轴于点
轴于点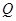 ,是否存在点
,是否存在点 使得
使得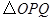 与
与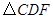 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本题9分)
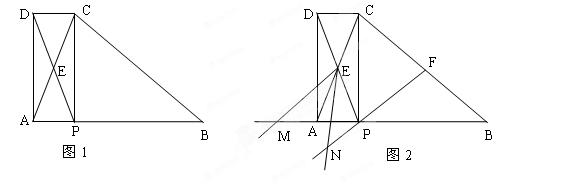
如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作□APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;
(2)□APCD是否为矩形?请说明理由;
(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.
(本题8分)
网上报道入春以来山东蔬菜严重滞销.为了减少菜农的损失,政府部门出台了相关补贴政策:采取每吨补贴0.02万元的办法补偿菜农.
下图是某菜农今年政府补助前、后蔬菜销售总收入y(万元)与销售量x(吨)的关系图.请结合图象解答以下问题: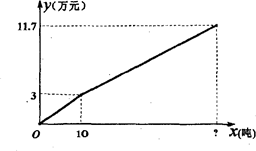
(1)在出台该项优惠政策前,蔬菜的售价为每吨多少万元?
(2)出台该项优惠政策后,该菜农将剩余蔬菜按原售价打九折赶紧全部销完,加上政府补贴共收入11.7万元,求菜农共销售了多少吨蔬菜?
(3)①求出台该项优惠政策后y与x的函数关系式;
②去年该菜农销售30吨,总收入为10.25万元;若按今年的销售方式,则至少要销售多少吨蔬菜,总收入才能达到或超过去年水平.
(本题6分)
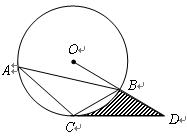
如图,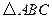 内接于⊙O,点
内接于⊙O,点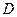 在半径
在半径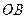 的延长线上,
的延长线上, .
.
(1)试判断直线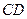 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧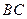 、线段
、线段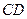 和
和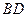 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留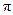 和根号).
和根号).
(本题8分)
某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角. 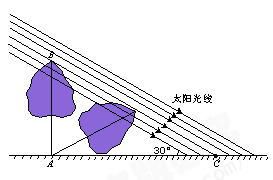
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变。①求树与地面成45°角时的影长。
②试求树影的最大长度.
(计算结果精确到0.1米,参考数据: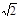 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)