某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
| 价格x(元/个) |
… |
30 |
40 |
50 |
60 |
… |
| 销售量y(万个) |
… |
5 |
4 |
3 |
2 |
… |
同时,销售过程中的其他开支(不含造价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
抛物线 ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线 交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线
交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线 (
( )交边AB于点N.若△OAN的面积是4,求△OMN的面积.
)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
先化简,再求值: ,其中
,其中 ,
, .
.
面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a= .
.
①求点D的坐标及该抛物线的解析式.
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由.
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围.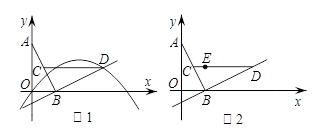
问题背景:已知在△ABC中,AB边上的动点D由A向B运动(与A,B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连结DE交AC于点F,点H是线段AF上一点
(1)初步尝试:如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等,求证:HF=AH+CF
小王同学发现可以由以下两种思路解决此问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立.
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分)
(2)类比探究:如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 :1,求
:1,求 的值.
的值.
(3)延伸拓展:如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).