面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a= .
.
①求点D的坐标及该抛物线的解析式.
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由.
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围.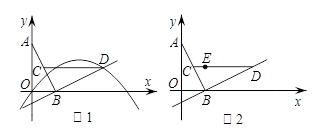
在平面直角坐标系中,顺次连结A(-2,0)、B(4,0)、C(-2,-3)各点,试求:A、B两点之间的距离。
点C到X轴的距离。
△ABC的面积。

如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D。
试说明:AC∥DF。
解:因为∠1=∠2(已知)
∠1=∠3,∠2=∠4()
所以∠3=∠4(等量代换)
所以∥()
所以∠C=∠ABD,()
又因为∠C=∠D(已知)
所以∠D=∠ABD(等量代换)
所以 AC∥DF()
如图,已知直线 被直线
被直线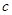 所截,
所截, ∥
∥ ,如果
,如果 ,求∠1的度数。
,求∠1的度数。
某农场 名职工耕种
名职工耕种 公顷土地,分别种植水稻、蔬菜和棉花,种植这些农作物每公顷所需人数如表1;另外设水稻和蔬菜的种植面积分别为
公顷土地,分别种植水稻、蔬菜和棉花,种植这些农作物每公顷所需人数如表1;另外设水稻和蔬菜的种植面积分别为 公顷、
公顷、 公顷,每公顷各种农作物预计产值如表2。
公顷,每公顷各种农作物预计产值如表2。
用含
 的式子表示
的式子表示 。
。为完成国家的粮食任务,水稻、蔬菜和棉花的种植面积至少需要12公顷,且水稻、蔬菜和棉花的种植面积均为整数,那么水稻、蔬菜和棉花的种植面积应各为多少公顷?请安排出种植方案。
若设总产值为
 ,那么怎样安排种植面积才能取得最大效益?
,那么怎样安排种植面积才能取得最大效益?
在平原上有一条笔直的公路,在公路同侧有A、B两个村庄。若以公路为 轴建立平面直角坐标系,如图1:已知A、B两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P)在
轴建立平面直角坐标系,如图1:已知A、B两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P)在 轴上行驶.
轴上行驶.汽车行驶过程中到A、B两村距离之和最小为多少?
汽车行驶过程中到A、B两村距离之差最大为多少?
