如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).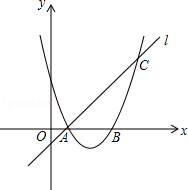
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;
(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.
已知,如图,在 ABCD中,E、F是对角线AC上的两点,且AE=CF,
ABCD中,E、F是对角线AC上的两点,且AE=CF,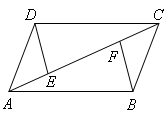
求证:DE=BF
如图所示,有一条小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,则这条小路的面积是多少?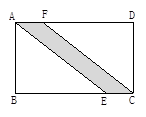
已知m=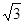 -2,求代数式m2+4m-9的值.
-2,求代数式m2+4m-9的值.
已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上.的一个定点(如图1)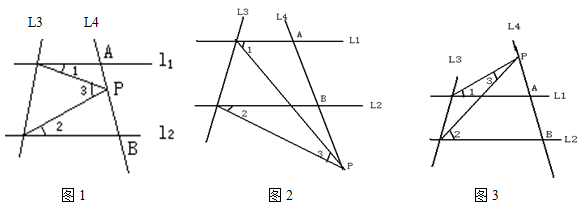
(1)写出∠1、∠2、∠3、之间的关系并说出理由。
(2)如果点P为线段AB上.的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(不必说理由)
(3)如果点P在A、B两点外侧运动时, (点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由。
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
如图所示的长方形或正方形三类卡片各有若干张,请你用这些卡片,拼成一个面积是2a2+3ab+b2长方形(要求:所拼图形中每类卡片都要有,卡片之间不能重叠。)
画出示意图,并计算出它的面积。