图(甲)为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n =100匝、电阻r =10W,线圈的两端经集流环与电阻R连接,电阻R =" 90" Ω,与R并联的交流电压表为理想电表。在t =0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量F随时间t按图15(乙)所示正弦规律变化。 求: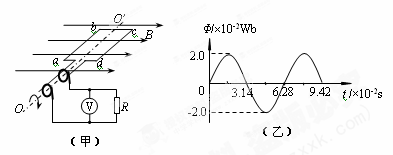
(1) 从1.57×10-2s到4.71×10-2s内通过电阻R上的电量q。
(2)电路中交流电压表的示数。
(3)线圈匀速转动一周的过程中,外力所做的功W外。
如图所示,一个底面粗糙、质量为M的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成θ=30°角;现用一端固定的轻绳系一质量为m的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为θ=30°,试求绳子对小球拉力FT和地面对劈的摩擦力Ff。
在如图所示的电路中,两平行正对金属板A、B水平放置,两板间的距离d=4.0cm。电源电动势E=400V,内电阻r=20Ω,电阻R1=1980Ω。闭合开关S,待电路稳定后,将一带正电的小球(可视为质点)从B板上的小孔以初速度v0=1.0m/s竖直向上射入两板间,小球恰好能到达A板。若小球所带电荷量q=1.0×10-7C,质量m=2.0×10-4kg,不考虑空气阻力,忽略射入小球对电路的影响,取g=10m/s2。求: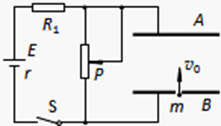
(1)A、B两金属板间的电压的大小U;
(2)滑动变阻器消耗的电功率P滑;
(3)电源的效率η;
(4)电源的最大输出功率。
如图所示电路中,电源电动势E=10V,内阻r=2Ω,电阻R1=12Ω,小灯泡L标有“6V 3W”。设灯丝的电阻不随温度变化,试求:
(1)开关S闭合后,电流表和电压表的示数;
(2)在电路中与R1并联一个定值电阻R2后,路端电压变为6V,求R2的大小。
有一平行板电容器倾斜放置,极板AB、CD与水平面夹角θ=45°,板间距离为d,AB板带负电、CD板带正电,如图所示,有一质量为m、电荷量大小为q的带电微粒,以动能EK0沿水平方向从下极板边缘A处进入电容器,并从上极板边缘D处飞出,运动轨迹如图中虚线所示,试求:
(1)带电徽粒的电性.
(2)两极板间的电势差.
(3)微粒飞出时的动能EK(重力加速度为g)
如图所示,质量为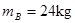 的木板B放在水平地面上,质量为
的木板B放在水平地面上,质量为 的木箱A放在木板B上.一根轻绳一端拴在木箱上,另一端拴在天花板上,轻绳与水平方向的夹角为θ=37°.已知木箱A与木板B之间的动摩擦因数
的木箱A放在木板B上.一根轻绳一端拴在木箱上,另一端拴在天花板上,轻绳与水平方向的夹角为θ=37°.已知木箱A与木板B之间的动摩擦因数 .现用水平向右、大小为200 N的力F将木板B从木箱A下面匀速抽出(sin 37°≈0.6,cos 37°≈0.8,重力加速度g取10 m/s2),则木板B与地面之间的动摩擦因数
.现用水平向右、大小为200 N的力F将木板B从木箱A下面匀速抽出(sin 37°≈0.6,cos 37°≈0.8,重力加速度g取10 m/s2),则木板B与地面之间的动摩擦因数 的大小是多少?
的大小是多少?