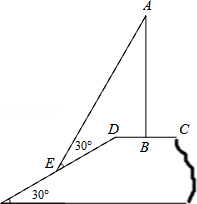
在与水平面夹角是30°的斜坡的顶部，有一座竖直的古塔，如图是平面图，斜坡的顶部CD是水平的，在阳光的照射下，古塔AB在斜坡上的影长DE为18米，斜坡顶部的影长DB为6米，光线AE与斜坡的夹角为30°，求古塔的高（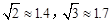
）．
如图，直线AC∥DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。
以下是他的想法，请你填上根据。小华是这样想的：
因为CF和BE相交于点O，
根据得出∠COB＝∠EOF；
而O是CF的中点，那么CO＝FO，又已知 EO＝BO，
根据得出△COB≌△FOE，
根据得出BC＝EF，
根据得出∠BCO＝∠F，
既然∠BCO＝∠F，根据出AB∥DF，
既然AB∥DF，根据得出∠ACE和∠DEC互补.
化简求值：
．
阅读理解：
方程ax2+bx+c=0（a≠0）的根是x=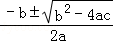
．
方程y2+by+ac=0的根是y=
．
因此，要求ax2+bx+c=0（a≠0）的根，只要求出方程y2+by+ac=0的根，再除以a就可以了．
举例：解方程72x2+8x+
=0．
解：先解方程y2+8y+72×=0，得y1=﹣2，y2=﹣6．
∴方程72x2+8x+=0的两根是x1=
，x2=
．
即x1=﹣
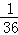，x2=﹣
．
请按上述阅读理解中所提供的方法解方程49x2+6x﹣
=0．
如图，在梯形ABCD中，DC∥AB，AD=BC，BD平分∠ABC，∠A=60°．过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF，求证：△DEF为等边三角形．
如图，在长为10cm，宽为8cm的矩形的四个角上截去四个全等的小正方形，使得留下的图形（图中阴影部分）面积是原矩形面积的80%，求所截去小正方形的边长．