如图,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=300的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数μ=0.1.,取g=10m/s2.求: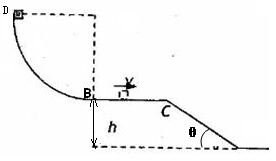
(1)小滑块刚到达圆弧的B点时对圆弧的压力;
(2)小滑块到达C点时速度的大小;
(3)小滑块从C点运动到地面所需的时间。
如图所示,水平虚线L1.L2间的高度差h=5cm,L1的上方和L2的下方都存在垂直
纸面向里的匀强磁场和竖直向上的匀强电场,下方磁场的磁感应强度是上方的 倍,一带
倍,一带
电微粒正好能在竖直平面内沿图中轨迹做周期性运动,在两磁场中的轨迹是半圆.当运动到
轨迹最低点时,如果撤去电场,微粒将做匀速直线运动.取g=10m/s2. 
说出微粒的绕行方向;
分别求出微粒在两磁场中的速度大小;
如图所示,ABD0是处于竖直平面内的光滑轨道,AB是半径为R=15m的14圆周轨道,半径OA处于水平位置,BD0是直径为l5m的半圆轨道,D为BD0轨道的中央。一个小球P从A点的正上方距水平半径0A高H处自由落下,沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的 倍.取g为10m/s2
倍.取g为10m/s2 H的大小
试讨论此球能否到达BD0轨道的0点,并说明理由;
据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,其半径r约为地球半径的2倍,假设有一艘飞船环绕该星球做匀速圆周运动,且飞行速度为v=8km/s。(地球的半径R=6400km,地球表面的重力加速度g=lOm/s2)求:该行星表面的重力加速度:
飞船到该星球表面的距离。(结果保留3位有效数字)
如图所示,质量为m的小车,静止在光滑的水平地面上,车长为L0,现给小车施加一个水平向右的恒力F,使小车向右做匀加速运动,与此同时在小车的正前方S0处的正上方H高处,有一个可视为质点的小球从静止开始做自由落体运动(重力加速度为g),问恒力F满足什么条件小球可以落到小车上?
如图所示,水平桌面上有一轻弹簧,左端固定在A点,处于自然状态时其右端位于B点.水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8 m的圆环剪去了左上角1350的圆弧,MN为其竖直直径,且P点到桌面的竖直距离也为R.用质量m1= 0.4 kg的可视为质点的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点.用同种材料、质量m2=0.2kg的可视为质点的物块将弹簧缓慢压缩到C点释放,物块通过B点后从B点运动到D点过程的位移与时间的关系为 ,物块飞离桌面边缘D点后由P点沿切线落入圆轨道.g="10" m/s2.
,物块飞离桌面边缘D点后由P点沿切线落入圆轨道.g="10" m/s2.
求DP间的水平距离s.
判断质量为m2的物块能否沿圆轨道到达M点.
质量为m2的物块在释放后的运动过程中克服摩擦力做的功。