给出下列四个命题:
①命题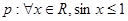 ,则
,则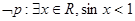 .
.
②当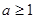 时,不等式
时,不等式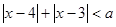 的解集为非空.
的解集为非空.
③当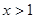 时,有
时,有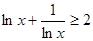 .
.
④设复数z满足(1-i)z="2" i,则z=1-i
其中真命题的个数是
| A.1 | B.2 | C.3 | D.4 |
已知抛物线y2=4x的准线与双曲线 -y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
-y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
A. B.
B. C.2D.
C.2D.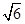
若双曲线 -
-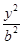 =1(a>0,b>0)上不存在点P,使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
=1(a>0,b>0)上不存在点P,使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
A.( ,+∞) ,+∞) |
B.[ ,+∞) ,+∞) |
C.(1, ] ] |
D.(1, ) ) |
若双曲线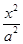 -
-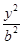 =1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
=1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
A.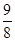 |
B.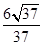 |
C.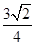 |
D.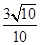 |
设抛物线x2=4y与椭圆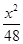 +
+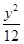 =1交于点E,F,则△OEF(O为坐标原点)的面积为( )
=1交于点E,F,则△OEF(O为坐标原点)的面积为( )
A.3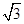 |
B.4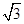 |
C.6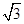 |
D.12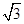 |
已知椭圆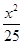 +
+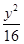 =1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,则下面结论正确的是( )
| A.P点有两个 | B.P点有四个 |
| C.P点不一定存在 | D.P点一定不存在 |