如图,已知 切⊙
切⊙ 于点E,割线PBA交⊙
于点E,割线PBA交⊙ 于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.
于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.
求证:(Ⅰ) ; (Ⅱ)
; (Ⅱ) .
.
已知各项均为整数的数列 满足
满足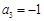 ,
, ,前6项依次成等差数列,从第5项起依次成等比数列.
,前6项依次成等差数列,从第5项起依次成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求出所有的正整数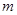 ,使得
,使得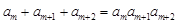 .
.
已知函数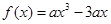 ,
,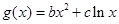 ,且
,且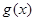 在点
在点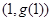 处的切线方程为
处的切线方程为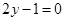 .
.
(1)求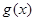 的解析式;
的解析式;
(2)求函数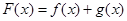 的单调递增区间.
的单调递增区间.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件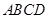 ,设梯形部件
,设梯形部件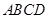 的面积为
的面积为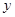 平方米.
平方米.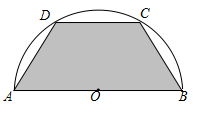
(1)按下列要求写出函数关系式:
①设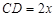 (米),将
(米),将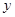 表示成
表示成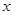 的函数关系式;②设
的函数关系式;②设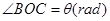 ,将
,将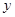 表示成
表示成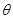 的函数关系式.
的函数关系式.
(2)求梯形部件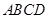 面积
面积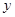 的最大值.
的最大值.
设在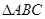 中,角
中,角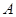 、
、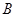 、
、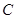 的对边分别为
的对边分别为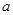 、
、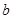 、
、 ,且
,且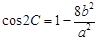 .
.
(1)求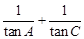 的值;
的值;
(2)若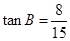 ,求
,求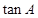 及
及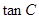 的值.
的值.
如图,在四棱锥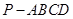 中,底面
中,底面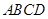 是直角梯形,
是直角梯形,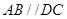 ,
,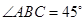 ,
,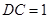 ,
,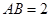 ,
,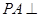 平面
平面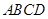 ,
,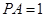 .
.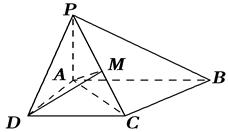
(1)求证: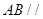 平面
平面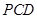 ;
;
(2)求证: 平面
平面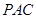 ;
;
(3)若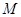 是
是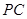 的中点,求三棱锥
的中点,求三棱锥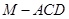 的体积.
的体积.