如图1,一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线OAB,如图2所示,量得连杆OA长为10cm,雨刮杆AB长为48cm,∠OAB=1200.若启动一次刮雨器,雨刮杆AB正好扫到水平线CD的位置,如图3所示.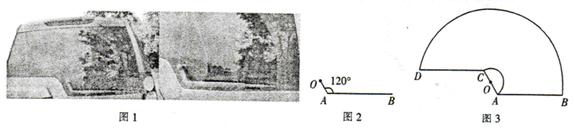
(1)求雨刮杆AB旋转的最大角度及O、B两点之间的距离;(结果精确到0.01)
(2)求雨刮杆AB扫过的最大面积.(结果保留π的整数倍)
(参考数据:sin60°=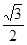 ,cos60°=
,cos60°=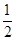 ,tan60°=
,tan60°=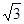 ,
,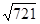 ≈26.851,可使用科学计算器)
≈26.851,可使用科学计算器)
解不等式组 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
计算: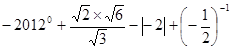 .
.
已知:把 和
和 按如图(1)摆放(点
按如图(1)摆放(点 与点
与点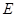 重合),点
重合),点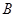 、
、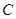 (
(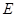 )、
)、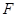 在同一条直线上.
在同一条直线上.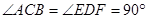 ,
,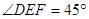 ,
,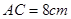 ,
,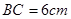 ,
,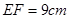 .如图(2),
.如图(2),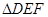 从图(1)的位置出发,以
从图(1)的位置出发,以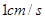 的速度沿
的速度沿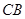 向
向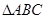 匀速移动,在
匀速移动,在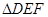 移动的同时,点
移动的同时,点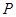 从
从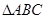 的顶点
的顶点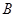 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿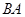 向点
向点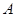 匀速移动.当
匀速移动.当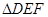 的顶点
的顶点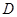 移动到
移动到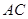 边上时,
边上时,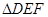 停止移动,点
停止移动,点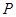 也随之停止移动.
也随之停止移动.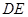 与
与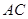 相交于点
相交于点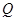 ,连接
,连接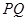 ,设移动时间为
,设移动时间为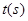
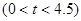 .
.

(1)当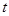 为何值时,点
为何值时,点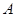 在线段
在线段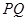 的垂直平分线上?
的垂直平分线上?
(2)连接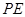 ,设四边形
,设四边形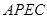 的面积为
的面积为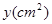 ,求
,求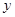 与
与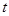 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻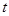 ,使面积
,使面积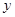 最小?若存在,求出
最小?若存在,求出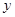 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻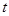 ,使
,使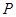 、
、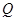 、
、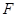 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时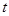 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)
如图,已知关于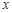 的一元二次函数
的一元二次函数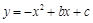 (
(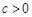 )的图象与
)的图象与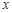 轴相交于
轴相交于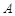 、
、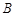 两点(点
两点(点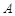 在点
在点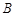 的左侧),与
的左侧),与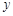 轴交于点
轴交于点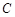 ,且
,且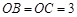 ,顶点为
,顶点为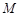 .
.
(1)求出一元二次函数的关系式;
(2)点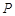 为线段
为线段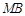 上的一个动点,过点
上的一个动点,过点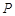 作
作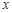 轴的垂线
轴的垂线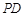 ,垂足为
,垂足为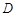 .若
.若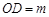 ,
,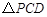 的面积为
的面积为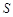 ,求
,求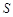 关于
关于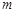 的函数关系式,并写出
的函数关系式,并写出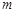 的取值范围;
的取值范围;
(3)在(2)的条件下,当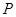 点坐标是时,
点坐标是时,  为直角三角形.
为直角三角形.
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.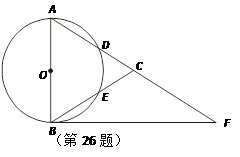
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为.