某农户承包果树若干亩，今年投资13800元，收获水果总产量为18000千克．此水果在市场上每千克售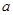
元，在果园直接销售每千克售
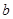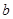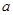元（＜）．该农户将水果拉到市场出售平均每天出售1000千克，需2人帮忙，每人每天付工资100元，农用车运费及其他各项税费平均每天200元．分别用含
，
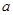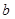的代数式表示两种方式出售水果的收入若
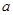=4.5元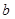，=4元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好．该农户加强果园管理，力争到明年纯收入达到72000元，而且该农户采用了（2）中较好的出售方式出售，那么纯收入增长率是多少（纯收入=总收入－总支出）？
已知，如图，二次函数y=ax2+2ax﹣3a（a≠0）图象的顶点为H，与x轴交于A、B两点（B在A点右侧），点H、B关于直线l：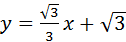
对称．
（1）求A、B两点坐标，并证明点A在直线l上；
（2）求二次函数解析式；
（3）过点B作直线BK∥AH交直线l于K点，M、N分别为直线AH和直线l上的两个动点，连接HN、NM、MK，求HN+NM+MK和的最小值．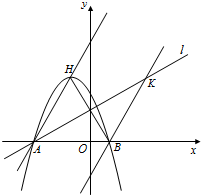
已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①
已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．
如图，在△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆分别与AB、AC边相切于D、E两点，连接OD．已知BD=2，AD=3．
求：（1）tanC；
（2）图中两部分阴影面积的和．
如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．
（1）求线段AB所在直线的函数解析式，并写出当0≤y≤2时，自变量x的取值范围；
（2）将线段AB绕点B逆时针旋转90°，得到线段BC，请在答题卡指定位置画出线段BC．若直线BC的函数解析式为y=kx+b，则y随x的增大而 （填“增大”或“减小”）．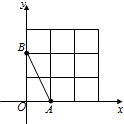
在结束了380课时初中阶段数学内容的教学后，唐老师计划安排60课时用于总复习，根据数学内容所占课时比例，绘制如下统计图表（图1～图3），请根据图表提供的信息，回答下列问题：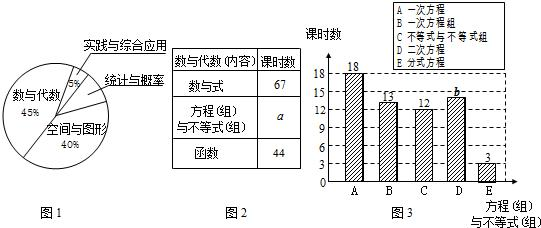
（1）图1中“统计与概率”所在扇形的圆心角为 度；
（2）图2、3中的a= ，b= ；
（3）在60课时的总复习中，唐老师应安排多少课时复习“数与代数”内容？