如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.
求:(1)tanC;
(2)图中两部分阴影面积的和.
以平面上一点O为直角顶点,分别画出两个直角三角形,记作△AOB和△COD,其中∠ABO=∠DCO=30°.
(1)点E、F、M分别是AC、CD、DB的中点,连接EF和FM.
①如图1,当点D、C分别在AO、BO的延长线上时, =_______;
=_______;
②如图2,将图1中的△AOB绕点O沿顺时针方向旋转 角(
角( ),其他条件不变,判断
),其他条件不变,判断 的值是否发生变化,并对你的结论进行证明;
的值是否发生变化,并对你的结论进行证明;
(2)如图3,若BO= ,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
已知关于x的方程 .
.
(1)当k取何值时,方程有两个实数根;
(2)若二次函数 的图象与
的图象与 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
(3)若(2)中的抛物线与x轴交于A、B两点,与y轴交于C点.将抛物线向上平移n个单位,使平移后得到的抛物线的顶点落在△ABC的内部(不包括△ABC的边界),写出n的取值范围.
老师要求同学们在图①中 内找一点P,使点P到OM、ON的距离相等.
内找一点P,使点P到OM、ON的距离相等.
小明是这样做的:在OM、ON上分别截取OA=OB,连结AB,取AB中点P,点P即为所求.
请你在图②中的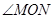 内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
内找一点P,使点P到OM的距离是到ON距离的2倍.要求:简单叙述做法,并对你的做法给予证明.
如图,在Rt△ABC中,∠ABO=90°,OB=4,AB=8,且反比例函数 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若
在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若 ,
,
(1)求反比例函数解析式;
(2)求C点坐标.
如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.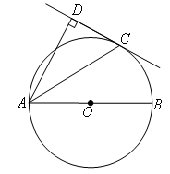
(1)求证:CD是⊙O的切线;
(2)若AC=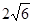 ,AD=4,求AB的长.
,AD=4,求AB的长.