如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立。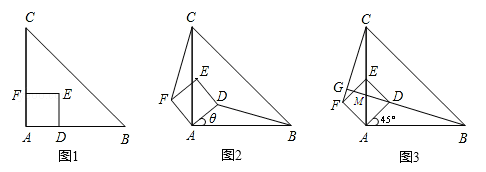
（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由。
（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G。
求证：BD⊥CF。
（3）在（2）小题的条件下, AC与BG的交点为M， 当AB=4，AD=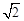
时，求线段CM的长。
点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点，点P从顶点A,点Q从顶点B同时出发，它们的速度都是1cm/s。
（1）经过1秒时，连接AQ、CP交于点M，则在P、Q运动的过程中，求证：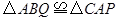
，并求出∠CMQ的度数；
（2）经过几秒时，△PBQ是直角三角形？
如图，在笔直的公路L的同侧有A、B两个村庄，已知A、B两村分别到公路的距离AC=3km，BD=4km。现要在公路上建一个汽车站P，使该车站到A、B两村的距离相等，
（1）试用直尺和圆规在图中作出点P；（保留作图痕迹）
（2）若连接AP、BP，测得∠APB=90°，求A村到车站的距离
如图所示，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积．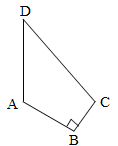
已知：如图，在△BAC中，AB=AC,，D,E分别为AB,AC边上的点，且DE∥BC，求证: △ADE是等腰三角形． 
已知：如图，点B、F、C、E在一条直线上，∠B＝∠E，∠ACB＝∠DFE，且BF=EC．求证：△ABC≌△DEF．