已知正方形ABCD中,边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶点的内接正方形的面积为y,求y与x的函数关系式,当x为何值时内接正方形的面积最小.
写出下列函数关系式,并指出关系式中的自变量和函数:
圆锥的底面半径为定值r,则圆锥的体积V与圆锥的高h之间的关系
已知□ABCD的对角线AC、BD相交于O,△AOB是等边三角形,AB=4cm,求这个平行四边形的面积。
如图所示,在正方形ABCD中,E是对角线AC上一点,EF垂直CD于F,EG垂直AD于G,求证BE=FG.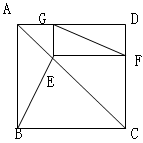
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF。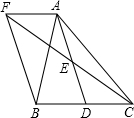
(1)求证:D是BC的中点
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论。