为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各10件样品，测量产品中某种元素的含量（单位：毫克）.如图是测量数据的茎叶图：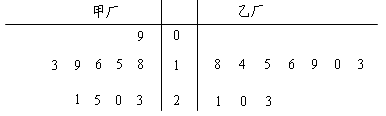
规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品.
（1）试用上述样本数据估计甲、乙两厂生产的优等品率；
（2）从乙厂抽出的上述10件样品中，随机抽取3件，求抽到的3件样品中优等品数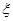
的分布列及其数学期望
；
（3）从甲厂的10件样品中有放回的随机抽取3件，也从乙厂的10件样品中有放回的随机抽取3件，求抽到的优等品数甲厂恰比乙厂多2件的概率．
求证：关于x的方程x2+2ax+b="0" 有实数根，且两根均小于2的充分但不必要条件是a≥2且|b| ≤4.
给定两个命题,
：对任意实数
都有
恒成立；
：关于的方程
有实数根；如果与中有且仅有一个为真命题，求实数
的取值范围
分别写出下列命题的逆命题，否命题，逆否命题，并判断其真假．
（1）矩形的对角线相等且互相平分；
（2）正偶数不是质数．
若F1、F2分别为双曲线 －＝1下、上焦点，O为坐标原点，P在双曲线的下支上，点M在上准线上，且满足：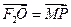
，
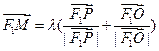
（1）求此双曲线的离心率；
（2）若此双曲线过N(，2)，求此双曲线的方程
（3）若过N(，2)的双曲线的虚轴端点分别B1，B2(B2在x轴正半轴上)，点A、B在双曲线上，且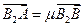
，求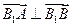
时，直线AB的方程．
如图，正四棱锥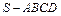
的高
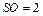，底边长
．求异面直线
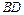和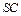
之间的距离．