设函数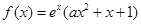 (
(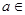 R),且该函数曲线
R),且该函数曲线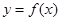 在
在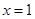 处的切线与
处的切线与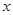 轴平行.
轴平行.
(Ⅰ)讨论函数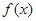 的单调性;
的单调性;
(Ⅱ)证明:当 时,
时,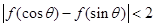 .
.
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为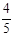 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为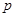 ,
, (
(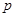 >
> ),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ |
0 |
1 |
2 |
3 |
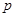 |
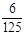 |
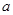 |
b |
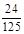 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求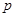 ,
, 的值;
的值;
(Ⅲ)求数学期望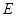 ξ.
ξ.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,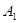 、
、 、
、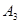 、
、 是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到N、M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.
是道路网中位于一条对角线上的4个交汇处,今在道路网M、N处的甲、乙两人分别要到N、M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.
(Ⅰ)求甲经过 的概率;
的概率;
(Ⅱ)求甲、乙两人相遇经 点的概率;
点的概率;
(Ⅲ)求甲、乙两人相遇的概率.
已知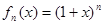 ,
,
(1)若 ,求
,求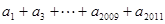 的值;
的值;
(2)若 ,求
,求 中含
中含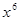 项的系数
项的系数
如图,一环形花坛分为A、B、C、D四块,要求在每块里种一种花,且相邻的2块种不同的花.
(1)若在三种花种选择两种花种植,有多少种不同的种法?
(2)若有四种花可供选择,种多少种花不限,有多少种不同的种法?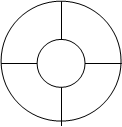
已知集合A= ,B=
,B= ,
,
(1)当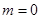 时,求
时,求
(2)若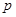 :
: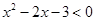 ,
,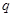 :
: ,且
,且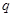 是
是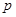 的必要不充分条件,求实数
的必要不充分条件,求实数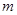 的取值范围.
的取值范围.